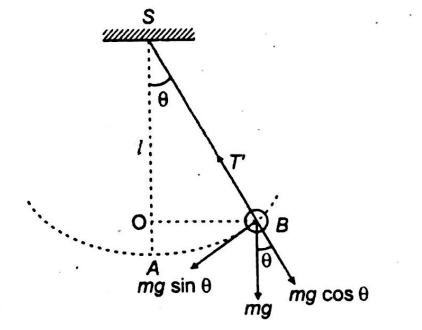
Question

A pendulum bob has a speed of $3 \,m/s$ at its lowest position. The pendulum is $0.5 \,m$ long. The speed of the bob, when length makes an angle of $60^{\circ}$ to the vertical, is :

• A. 2 m/s
• B. $\frac{1}{2}\,m/s$
• C. $ \frac{1}{3} m/s$
• D. 2.5 m/s

Answer 1

Answer: (A)

When a body oscillates in simple harmonic motion (SHM) it is acted upon by a restoring force which tends to bring it in the equilibrium position. Due to this force there is potential energy in the body. Also, as the body is in motion it has kinetic energy. During oscillation of the body, the two energies convert into each other but their sum remains constant.

P. E at $ B=m g(l-l \cos \theta)$
From law of conservation of energy, we have
$\frac{1}{2} m(3)^{2} =\frac{1}{2} m v^{2}+m g l(1-\cos \theta) $
$9 =v^{2}+2 g l\left(1-\cos 60^{\circ}\right)$
$9 =v^{2}+2 \times 10 \times 0.5\left(1-\frac{1}{2}\right)$
$\Rightarrow v^{2} =4 \,m / s $
$\therefore v =2 \,m / s$
Therefore, speed of bob is $2\, m / s$.