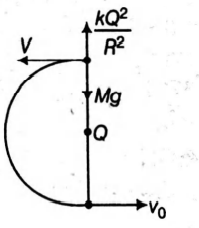
Question

A particle with charge $Q$ coulomb, tied at the end of an inextensible string of length $R$ meter, revolves in a vertical plane. At the centre of the circular trajectory there is a fixed charge of magnitude $Q$ coulomb. The mass of the moving charge $M$ is such that $Mg = \frac{Q^{2}}{4\pi\varepsilon_{0}R^{2}}.$ If at the highest position of the particle, the tension of the string just vanishes, the horizontal velocity at the lowest point has to be

• A. 0
• B. $2\sqrt{gR}$
• C. $\sqrt{2gR}$
• D. $\sqrt{5gR}$

Answer 1

Answer: (B)

According to the question, when tension in the string is zero.

As $T = 0$
$Mg - \frac{KQ^2}{R^2} = \frac{mv^2}{R} \,\, (k = \frac{1}{4\pi \varepsilon_0})$
$\frac{m v^{2}}{R}=$ centripetal force required to keep the body in a circular path
$\Rightarrow v=0 \,\,\,\left[\because M g=\frac{k Q^{2}}{R^{2}}\right]$
So the required work done to keep charge in vertical motion
$\therefore W_{8} =\Delta K E=$ change in $ K . E . $
$\Rightarrow m g(2 R) =\frac{1}{2} m v_{0}^{2} $
$v_{0}^{2} =2 g \cdot 2 R=4 g R $
$v_{0} =\sqrt{4 g R}=2 \sqrt{g R}$