Question

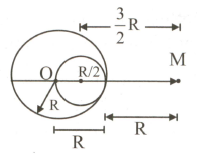
A particle placed at a distance $2R$ from the centre of a solid sphere of uniform density and radius $R$ experiences a gravitational force of attraction equal to $F_{1}$ . A spherical cavity of radius $\frac{R}{2}$ is now made in the sphere as shown in figure and the same particle now experiences a gravitational force $F_{2}$ . If the ratio $\frac{F_{1}}{F_{2}}$ is $\frac{x}{7}$ then find $x$ .

Answer 1

Mass of the cavity $=\frac{1}{8}$ of mass of sphere
$\Rightarrow M_{c}=\frac{M_{s}}{8}$
$F _1=\frac{ GMm }{(2 R }=\frac{ GMm }{4 R ^2}$
$M_{c}=\frac{M_{s}}{8}$
$F_{2}=\frac{GMm}{4 R^{2}}-\frac{\frac{GMm}{8}}{\left(\frac{3}{2} R\right)^{2}}$
$=\frac{GMm}{R^{2}}\left[\frac{1}{4} - \frac{1}{18}\right]$
$=\frac{\text{ GMm }}{R^{2}}\left[\frac{18 - 4}{72}\right]=\frac{7}{36}\frac{GMm}{R^{2}}$
$\frac{F_{1}}{F_{2}}=\frac{G M m}{\frac{7}{36} \frac{G M m}{R^{2}}}=\frac{9}{7}=1.29$