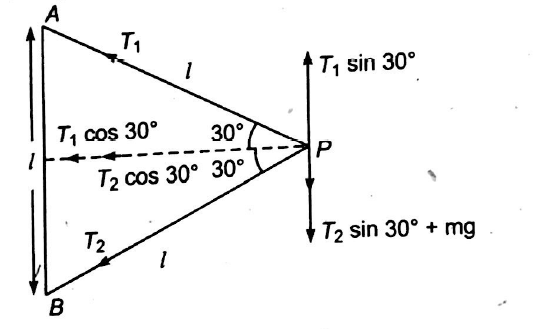
Question

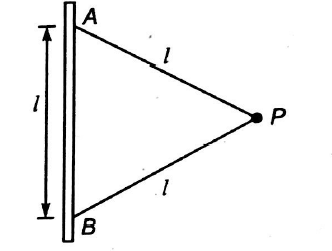
A particle $P$ of mass $m$ is attached to a vertical axis by two strings $AP$ and $BP$ of length I each as shown in the figure. The separation $A B$ rotates around the axis with an angular velocity $\omega$. The tension in the two strings are $T_{1}$ and $T_{2}$. Then

(1) $T_{1}-T_{2}=2 m g$
(2) $T_{1}+T_{2}=m \omega^{2} l$
(3) $T_{1}=T_{2}$
(4) $T_{1}+T_{2}=m g$

• A. 1, 2 and 3 are correct
• B. 1 and 2 are correct
• C. 2 and 4 are correct
• D. 1 and 3 are correct

Answer 1

Answer: (B)

Let $T_{1}$ and $T_{2}$ be the tensions in $PA$ and $PB$ respectively.

From the figure,
$T_{1} \sin 30^{\circ}=T_{2} \sin 30^{\circ}+m g$
or $T_{1}-T_{2}=2 m g \ldots$...(i)
and $T_{1} \cos 30^{\circ}+T_{2} \cos 30^{\circ}=m \omega^{2} l$
or $T_{1}+T_{2}=m \omega^{2} l \ldots$...(ii)
From Eqs. (i) and (ii)
$T_{1}=\frac{m}{2}\left[\omega^{2} l+2 g\right]$
and $T_{2}=\frac{m}{2}\left[\omega^{2} l-2 g\right]$