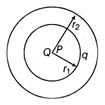
Q. A particle of positive charge $Q$ is fixed at point $P$. A second particle of mass m and negative charge $-\,q$ moves at constant speed in a circle of radius $ r_{1} $ , centered at $P$. The work $W$ that must be done by an external agent on the second particle to increase the radius of the motion to $ r_{2} $ , is given by
AMUAMU 2013Electrostatic Potential and Capacitance
Solution:
Force at $P$ due to $q$ when the radius of circle is
$F_{1}=\frac{Q q}{4 \pi \varepsilon_{0} r_{1}^{2}}$.... (i)
Force at $P$ due to $q$ when the radius of circle is
$F_{2}=\frac{1}{4 \pi \varepsilon_{0}} \frac{Q q}{r_{1}^{2}} \ldots$.. (ii)
Increase in radius $\left(r_{2}-r_{1}\right)$ (distance)
Resultant force $=\sqrt{F_{1} \times F_{2}}=\frac{1}{4 \pi \varepsilon_{0}} \frac{Q q}{r_{1} r_{1}^{2}}$
$ \therefore $ Work done $W=F \times d r$
$=\frac{1}{4 \pi \varepsilon_{0}} \frac{Q q}{r_{1} r_{2}} \times\left(r_{2}-r_{1}\right)$
$ W=\frac{Q q}{4 \pi \varepsilon_{0}}\left(\frac{1}{r_{1}}-\frac{1}{r_{2}}\right)$