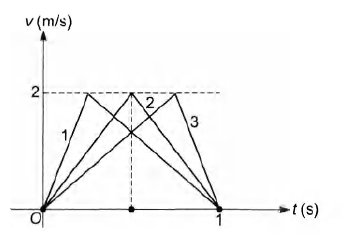
Question

A particle of mass $m$ moves on the $x$-axis as follows : it starts from rest at $t = 0$ from the point $x = 0$ and comes to rest at $t = 1$ at the point $x = 1$. No other information is available about its motion at intermediate times $(0 < t < 1)$. If a denotes the instantaneous acceleration of the particle, then

• A. $\alpha$ cannot remain positive for all $t$ in the interval 0 $\le t \le 1$
• B. $|\alpha|$ cannot exceed 2 at any point in its path
• C. $|\alpha|$ must be $\ge$ 4 at some point or points in its path
• D. $\alpha$ must change sign during the motion, but no other
  assertion can be made with the information given

Answer 1

Answer: (A)

Since, the body is at rest at $x = 0$ and $x = 1$ Hence, a cannot
be positive for all time in the interval 0$ \le t \le 1$
Therefore, first the particle is accelerated and then retarded.
Now, total time $t = 1\, s$ (given)
Total displacement $s = 1\, m$ (given)
$s$ = Area under $v-t$ graph
$\therefore $ Hight or $v_{max} =\frac{2s}{t}=2\,m/s $ is also fixed
[Aera or $s=\frac{1}{2} \, \times t \times v_{max}$]
If height and base are fixed, area is also fixed .
In case 2 : Acceleration = Retardation $= 4\, m/s^2$
In case 1 : Acceleration $> 4\, m/s^2$ while
Retardation $< 4\,m/s^2$
While in case 3 : Acceleration $< 4\,m/s^2$ as
Retardation $> 4\,m/s^2$
Hence,$|\alpha| \ge 4$ at some point or points in its path.