Q. A particle of mass ' $m$ ' is projected with a velocity $v$ making an angle of $30^{\circ}$ with the horizontal. The magnitude of angular momentum of the projectile about the point of projection when the particle is at its maximum height ' $h$ ' is
BITSATBITSAT 2013
Solution:
Given: A particle of mass $m$ is projected with a velocity $v$ making an angle of 30 with the horizontal.
To find the magnitude of the angular momentum of the projectile about the point of projection when the particle is at its maximum height $h$
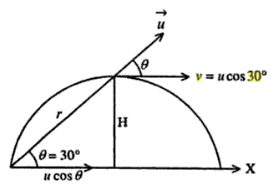
Let the velocity of the projection be $v$ and angle of projection be $\theta=30^{\circ}$
Angular momentum, $\vec{ L }=\vec{ r } \times m \vec{ v }$
$\Rightarrow |\vec{ L }|= rmv \sin \theta$
At maximum point, velocity is
$v = v \cos \theta= v \cos (30)=\frac{\sqrt{3} v }{2}$
only (direction: towards horizontal) and no vertical velocity is present.
The maximum height reached will be
$h=\frac{v^{2} \sin ^{2} \theta}{2 g}$
$\Rightarrow h=\frac{v^{2} \sin ^{2}\left(30^{\circ}\right)}{2 g}$
$\Rightarrow h =\frac{ v ^{2}}{8 g }$
From the figure,
$L =r m v \sin \theta$
$\Rightarrow L=m v h$
$\Rightarrow L=m \times \frac{\sqrt{3} v}{2} \times \frac{v^{2}}{8 g}$
$\Rightarrow L=\frac{\sqrt{3} m v^{3}}{16 g}$
is the magnitude of the angular momentum of the projectile about the point of projection when the particle is at its maximum height $h$.