Question

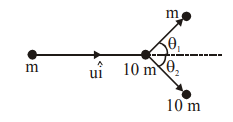
A particle of mass $m$ is moving along the $x$ -axis with initial velocity $u\hat{i } $. It collides elastically with a particle of mass $10 m$ at rest and then moves with half its initial kinetic energy (see figure). If $\sin \theta_{1}=\sqrt{n} \sin \theta_{2}$ then value of $n$ is___

Answer 1

By momentum conservation along y :
$m _{1} u _{1} \sin \theta_{1}= m _{2} u _{2} \sin \theta_{2} $
$\text { i.e. } mu _{1} \sin \theta_{1}=10 mu _{2} \sin \theta_{2} $
$ \Rightarrow u _{1} \sin \theta_{1}=10 u _{2} \sin \theta_{2} \,\,\,\,\, .....(i)$
$kf _{ m _{1}}=\frac{1}{2} ki _{ m _{1}}$ i.e. $ \frac{1}{2} mu _{1}^{2}=\frac{1}{2} \times \frac{1}{2} mu ^{2}$
i.e. $u _{1}=\frac{ u }{\sqrt{2}} \,\,\,\,\, ....(ii)$
Also collision is elastic $: k _{ i }= k _{ f }$
$\frac{1}{2} mu ^{2}=\frac{1}{2} mu _{1}^{2}+\frac{1}{2} . 10 m . u _{2}^{2}$
$\frac{1}{2} m u^{2}=\frac{1}{2} \times \frac{1}{2} m u^{2}+\frac{1}{2} \times 10 m . u_{2}^{2}$
$\frac{1}{4} mu ^{2}=\frac{1}{2} \times 10 \times mu _{2}^{2}$
$u _{2}=\frac{ u }{\sqrt{20}} \,\,\,\,\,\, ....(iii)$
Putting $(ii)$ & $(iii)$ in $(i)$
$\frac{ u }{\sqrt{2}} \sin \theta_{1}=10 .\frac{ u }{\sqrt{20}} \sin \theta_{2}$
$\sin \theta_{1}=\sqrt{10} \sin \theta_{2}$