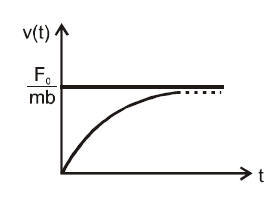
Q. A particle of mass $m$ is at rest at the origin at time $t = 0$. It is subjected to a force $F(t) = F_0e^{-bt}$ in the $x$ direction. Its speed $v(t)$ is depicted by which of the following curves ?
AIEEEAIEEE 2012Laws of Motion
Solution:
$F = ma = F_{0} e^{-bt}$
$\frac{dv}{dt}=\frac{F_{0}}{m} e^{-bt}$
$\int\limits^v_{{0}}$$dv=\frac{F_{0}}{m}$$\int\limits^t_{{0}}$$e^{-bt}dt$
$v=\frac{F_{0}}{m}\left[\frac{e^{-bt}}{-b}\right]^{t}_{_{_0}}$
$v=\frac{F_{0}}{mb}\left(1-e^{-bt}\right)$