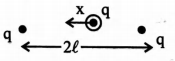Question

A particle of mass $m$ and charge $q$ is located midway between two fixed charged particles each having a charge $q$ and a distance $2 \ell$ apart. If it is displaced along the line connecting them and released. Also find its time period for SHM.

• A. $4 \pi \sqrt{\frac{ m \pi \epsilon_{0} \ell^{3}}{ q ^{2}}}$
• B. $\pi \sqrt{\frac{m \pi \epsilon_{0} \ell^{3}}{2 q^{2}}}$
• C. $2 \pi \sqrt{\frac{m \pi \epsilon_{0} \ell^{3}}{q^{2}}}$
• D. $\pi \sqrt{\frac{2 m \pi \epsilon_{0} \ell^{3}}{q^{2}}}$

Answer 1

Answer: (C)

When the charge is displaced by an amount $x$. Force on it
$F=\frac{K q^{2}}{(\ell+x)^{2}}-\frac{K q^{2}}{(\ell-x)^{2}}$
$=\frac{K q^{2}}{\left[\ell^{2}-x^{2}\right]^{2}}(-4 \ell x)$
or $F =-\frac{4 K \ell xq ^{2}}{\left(\ell^{2}- x ^{2}\right)^{2}}$
$=-\frac{\ell xq ^{2}}{\pi \epsilon_{0}\left(\ell^{2}- x ^{2}\right)^{2}}$
When $x$ is very small
$F=-\frac{q^{2}}{\pi \epsilon_{0} \ell^{3}} x$
or $a=-\frac{q^{2}}{\pi \epsilon_{0} m \ell^{3}} x$
$\omega^{2}=\frac{ q ^{2}}{\pi \epsilon_{0} m \ell^{3}} \& T =\frac{2 \pi}{\omega}$
$\omega=\frac{q}{\sqrt{\pi \varepsilon_{0} m \ell^{3}}}$
$T =2 \pi \sqrt{\frac{\pi \varepsilon_{0} m \ell^{3}}{ q ^{2}}}$