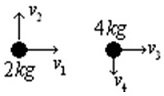
Question

A particle of mass $\text{2 kg}$ moving with a speed of $\text{6 m/s}$ collides elastically with another particle of mass $\text{4 kg}$ traveling in same direction with a speed of $\text{2 m/s}$ . The maximum possible deflection of the $\text{2 kg}$ particle is

• A. $37^{0}$
• B. $45^{0}$
• C. $53^{0}$
• D. $60^{0}$

Answer 1

Answer: (C)

Let situations after collision for balls are

According to question $2v_{1}+4v_{3}=20$
$2v_{2}=4v_{4}$
$\frac{1}{2}\times 2\left(v_{1}^{2} + v_{2}^{2}\right)+\frac{1}{2}\times 4\left(v_{3}^{2} + v_{4}^{2}\right)=\frac{1}{2}\times 2\times \left(6\right)^{2}+\frac{1}{2}\times 4\times \left(2\right)^{2}=44$
i.e. $v_{1}^{2}+v_{2}^{2}+2v_{3}^{2}+\frac{v_{2}^{2}}{2}=44$
i.e. $v_{1}^{2}+\frac{3}{2}v_{2}^{2}+\left(\frac{10 - v_{1}}{2}\right)^{2} \, 2=44$
i.e. $2v_{1}^{2}+3v_{2}^{2}+100-20v_{1}+v_{1}^{2}=88$
i.e. $3v_{1}^{2}+3v_{2}^{2}-20v_{1}+12=0$
i.e. $\frac{12}{v_{1}^{2}}-\frac{20}{v_{1}}+\frac{3 v_{2}^{2}}{v_{1}^{2}}+3=0$
Quadratic in $\frac{1}{v _{1} \, }$ which is real
$\therefore D\geq 0 \, \therefore \left(- 20\right)^{2}-4\times 12\left(1 + \frac{v_{2}^{2}}{v_{1}^{2}}\right)\times 3\geq 0$
$\therefore \, \, 1+\frac{v_{2}^{2}}{v_{1}^{2}}\leq \frac{400}{144}$
$\frac{v_{2}^{2}}{v_{1}^{2}}\leq \frac{256}{144}$
$-\frac{16}{12}\leq \frac{v_{2}}{v_{1}}\leq \frac{16}{12}\Rightarrow k=tan \theta \leq \frac{4}{3} \Rightarrow \theta \leq 53^{o}$