Q. A particle of mass $1\, kg$ is moving along the line $y=x+2$ (here $x$ and $y$ are in metres) with speed $2\, m / s$ The magnitude of angular momentum of particle about its origin is
System of Particles and Rotational Motion
Solution:
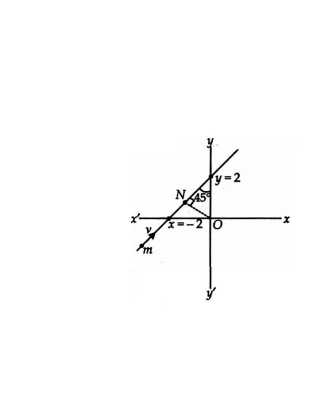
The given eqn. of the line is $y=x+2$.
At $x=-2, y=0$ and at $\,\,\, x=0, y=2$
The line is drawn as shown in the
figure.
Length of perpendicular drawn
from origin to this line is
$O N=r_{\perp}=\frac{0+0+2}{\sqrt{1^{2}+1^{2}}}=\sqrt{2}$
Angular momentum of particle about
$L=m v r_{1}=(1)(2) \sqrt{2}=2 \sqrt{2}\, kg\, m ^{2}\, s ^{-1}$