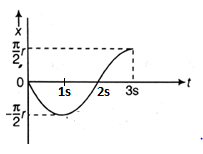
Question

A particle moves according to the law $x=rcos \frac{\pi t}{2}$ . The distance covered by it in the time interval between $t=0$ and $t=3 \, s$ is $nr$ . What is the value of $n$ ?

Answer 1

Given, $x=rcos \frac{\pi t}{2}$
$\Rightarrow v=\frac{d x}{d t}$
$=-\frac{\pi }{2}rsin \frac{\pi t}{2}$
Graphically it can be represented as shown in figure.

Distance covered by the particle
$=$ Magnitude of area of $x-t$ curve between
$0$ to $2 s$ and $2$ to $3 s$
$=\displaystyle \int _{0}^{2} v d t+\displaystyle \int _{2}^{3} v d t$
$=\left|- \displaystyle \int _{0}^{2} \frac{\pi }{2} r sin \frac{\pi }{2} t \, d t\right|+\left|\displaystyle \int _{2}^{3} - \frac{\pi }{2} r \, sin ⁡ \frac{\pi }{2} t \, d t\right|$
$=\left|\frac{- \pi }{2} r \displaystyle \int _{0}^{2} sin \frac{\pi t}{2} d t\right|+\left|\frac{- \pi }{2} r \displaystyle \int _{2}^{3} sin ⁡ \frac{\pi }{2} t \, d t\right|$
$=\left|\left[\frac{\pi r}{2} \frac{cos \frac{\pi t}{2}}{\frac{\pi }{2}}\right]_{0}^{2}\right|+\left|\left[\frac{\pi r}{2} \frac{cos ⁡ \frac{\pi }{2} t}{\frac{\pi }{2}}\right]_{2}^{3}\right|$
$=\left|r \left(cos \pi - cos ⁡ 0\right)\right|+\left|r \left(cos ⁡ \frac{3 \pi }{2} - cos ⁡ \pi \right)\right|$
$=r\left|- 1 - 1\right|+r\left|0 - \left(- 1\right)\right|=2r+r=3r$