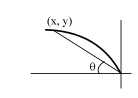
Q. A particle move from right to left along the parabola $y=\sqrt{-x}$ in such a way that $x$-coordinate (measured in meters) decreases at the rate of $8 \mathrm{~m} / \mathrm{sec}$. At the moment when $\mathrm{x}=-4$ the rate at which the angle of inclination $\theta$ of the line joining the particle to the origin is changing, is
Application of Derivatives
Solution:
$ y=\sqrt{-x} ; \tan \theta=\frac{y}{x}$
$\tan \theta=\frac{\sqrt{-x}}{x}=\frac{1}{\sqrt{-x}}$ $\sec ^{2} \theta \frac{\mathrm{d} \theta}{\mathrm{dt}}=+\frac{1}{2} \frac{1}{(-\mathrm{x})^{3 / 2}} \frac{\mathrm{dx}}{\mathrm{dt}}=\frac{1}{16} \cdot(-8) ($ where $\mathrm{x}=-4)$
$\sec ^{2} \theta \frac{\mathrm{d} \theta}{\mathrm{dt}}=-\frac{1}{2}$
Also where $\mathrm{x}=-4, \tan \theta=\frac{2}{-4}=-\frac{1}{2}$
$\therefore \left(1+\tan ^{2} \theta\right) \frac{\mathrm{d} \theta}{\mathrm{dt}}=-\frac{1}{2}$
$\frac{5}{4} \frac{\mathrm{d} \theta}{\mathrm{dt}}=-\frac{1}{2} \Rightarrow \frac{\mathrm{d} \theta}{\mathrm{dt}}=\frac{-2}{5}=-0.4$.