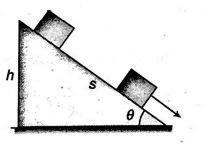
Question

A particle is released from the top of two inclined rough surfaces of height ' $h$ ' each. The angle of inclination of the two planes are $30^{\circ}$ and $60^{\circ}$ respectively. All other factors (e.g. coefficient of friction, mass of block etc.) are same in both the cases. Let $K_{1}$ and $K_{2}$ be the kinetic energies of the particle at the bottom of the plane in two cases. Then

• A. $K_{1} = K_{2}$
• B. $K_{1} > K_{2}$
• C. $K_{1} < K_{2}$
• D. data insufficient

Answer 1

Answer: (C)

Work done in friction is
$W =(\mu m g \cos \theta) s $
$=(\mu m g \cos \theta)\left(\frac{h}{\sin \theta}\right)=\mu m g h \cot \theta$
Now $\cot \theta_{1}=\cot 30^{\circ}=\sqrt{3}$
and $\cot \theta_{2}=\cot 60^{\circ}=\frac{1}{\sqrt{3}}$
$\therefore W_{1}>W_{2}$
i.e., kinetic energy in first case will be less.
$(K=m g h-W)$
Or $K_{1} < K_{2}$