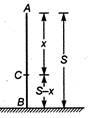
Q. A particle is released from a height $ S $ . At certain height its kinetic energy is three times its potential energy. The height and speed of the particle at that instant are respectively
Solution:
We can realise the situation as shown. Let at point C distance $ x $ from highest point A, the particles kinetic energy is three times its potential energy.
Velocity at C, $ {{v}^{2}}=0+2gx $ or $ {{v}^{2}}=2gx $ ...(i)
Potential energy at C $ =mg(S-x) $ ...(ii)
At point C, Kinetic energy
$ =3\times $ potential energy ie,
$ \frac{1}{2}m\times 2gx=3\times mg(S-x) $ or $ x=3S-3x $
or $ 4x=3S $
or $ S=\frac{4}{3}x $
or $ x=\frac{3}{4}S $
Therefore, from Eq. (i) $ {{v}^{2}}=2g\times \frac{3}{4}S $
Or $ {{v}^{2}}=\frac{3}{2}gS $
or $ V=\sqrt{\frac{3}{2}gS} $
Height of the particle from the ground
$ =S-x $
$ =S-\frac{3}{4} S=\frac{S}{4} $