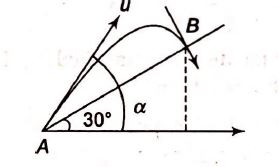
Question

A particle is projected with a certain velocity at an angle $\alpha$ above the horizontal from the foot of an inclined plane of inclination 30°. If the particle strikes the plane normally then $\alpha$ is equal to:

• A. $30^{\circ}+tan^{-1} \left(\frac{\sqrt{3}}{2}\right)$
• B. $45^{\circ}$
• C. $60^{\circ}$
• D. $30^{\circ} +tan^{-1} \left(2\sqrt{3}\right)$

Answer 1

Answer: (A)

$t_{AB} =$ time of flight of projectile
$=\frac{2u \,sin\left(\alpha-30^{\circ}\right)}{g\, cos\, 30^{\circ}}$
Now component of velocity along the plane becomes zero at point B.

$\theta =u cos\left(\alpha-30^{\circ}\right)-g \,sin\, 30^{\circ} \times T$
or $u \,\cos \left(\alpha-30^{\circ}\right) $
$=g \,sin\, 30^{\circ} \times \frac{2u \,sin \left(\alpha-30^{\circ}\right)}{g \,cos \,30^{\circ}}$
or $tan\left(\alpha-30^{\circ}\right)=\frac{cot \,30^{\circ}}{2} =\frac{\sqrt{3}}{2} $
$\alpha=30^{\circ} +tan^{-1}\left(\frac{\sqrt{3}}{2}\right)$