Q.
A particle is projected up from a point at an angle
$\theta$ with the horizontal direction. At any time $t$, if $p$ is the linear momentum, $y$ is the vertical displacement, $x$ is horizontal displacement, the graph among the following which does not represent the variation of kinetic energy $KE$ of the particle is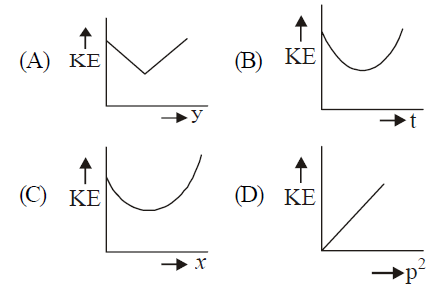
VITEEEVITEEE 2009
Solution:




