Q.
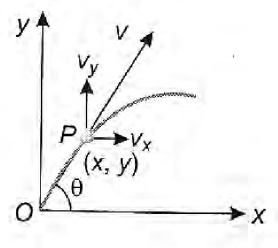
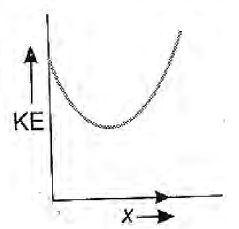
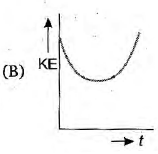
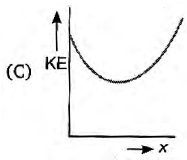
A particle is projected up from a point at an angle $\theta$ with the horizontal direction. At any time $t$, if $P$ is the linear momentum, $y$ is the vertical displacement, $x$ is horizontal displacement, the graph among the following which does not represent the variation of kinetic energy KE of the particle is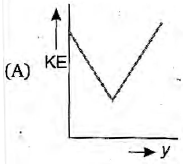
BITSATBITSAT 2009
Solution:
Momentum, $p=m.v$
$\Rightarrow v=\left( \frac{p}{m} \right)$
Kinetic energy, $KE=\frac{1}{2}m{{v}^{2}}$
$=\frac{1}{2}m\left( \frac{{{p}^{2}}}{{{m}^{2}}} \right)=\frac{1}{2m}{{p}^{2}}$
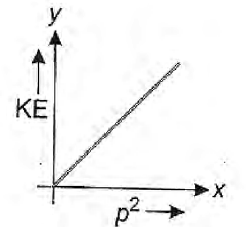
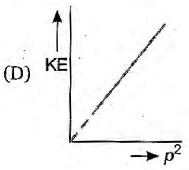
$\Rightarrow KE\,\propto \,{{p}^{2}} ( \because \frac{1}{2m}=$ constant)
Hence, the graph between KE and ${{p}^{2}}$ will be linear as shown below
Now, kinetic energy $KE=\frac{1}{2}\text{ }m{{v}^{2}}$
The velocity component at point $P$,
$v_{y}=(u\,\sin \theta -gt)$
and $v_{x} =u\,\,\cos \theta $
Resultant velocity at point $P$,
$\overrightarrow{v}=v_{y}\hat{j}+v_{x}\hat{i}$
$ =(u\,\sin \,\theta -gt)\hat{j}+u\cos \,\theta \,\hat{i}$
$|\overrightarrow{v}|=\sqrt{{{(u\,cos\,\theta )}^{2}}+{{(u\,\sin \theta -gt)}^{2}}}$
$=\sqrt{{{u}^{2}}{{\cos }^{2}}\theta +{{u}^{2}}\,{{\sin }^{2}}\,\theta +{{g}^{2}}{{t}^{2}}-2ugt\,\,\sin \theta }$
$\therefore \sqrt{{{u}^{2}}({{\cos }^{2}}\theta +{{\sin }^{2}}\theta )+{{g}^{2}}{{t}^{2}}-2ugt\,\sin \theta }$
$ KE=\frac{1}{2}m({{u}^{2}}+{{g}^{2}}{{t}^{2}}-2ugt\,\,\sin \theta )$
$ \Rightarrow KE\,\propto \,{{t}^{2}}$
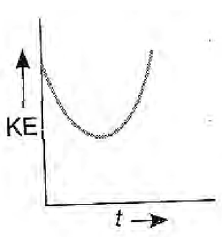
Hence, graph will be parabolic with intercept on y-axis.
Hence, the graph between KE and t
Now, in case of height $ KE=\frac{1}{2}m({{v}^{2}})$
and ${{v}^{2}}=({{u}^{2}}-2gy)$
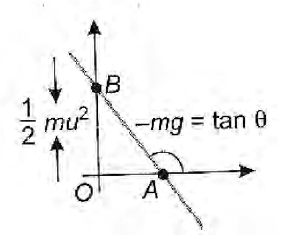
$\therefore KE=\frac{1}{2}m({{u}^{2}}-2gy)$
$KE=-mgy+\frac{1}{2}m{{u}^{2}}$
Now, $KE=\frac{1}{2}m{{v}^{2}}$
$KE=\frac{1}{2}m{{\left( \frac{x}{t} \right)}^{2}}$
$KE\,\propto \,{{x}^{2}}$.
Thus graph between KE and x will be parabolic.