Question

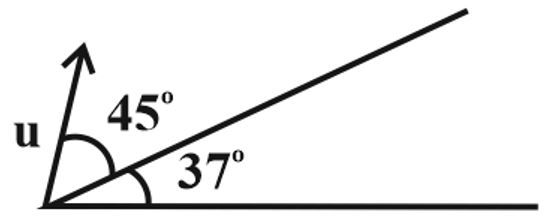
A particle is projected on a frictionless inclined plane of inclination $37^\circ $ at an angle of projection $45^\circ $ from the inclined plane as shown in the figure. If after the first collision from the plane, the particle returns to its point of projection, then what is the value of the reciprocal of the coefficient of restitution between the particle and the plane?

Answer 1

While going upward the time of flight is
$T =\frac{2 usin \alpha}{ g \cos \beta}$
So the range on the inclined plane is
$R =( u \cos \alpha) T -\frac{1}{2}(g \sin \beta) T ^{2}$
Just after the collision of the projectile with the inclined plane, the components of its velocity down the inclined plane and perpendicular to the inclined plane are
$v _{\|}=( g \sin \beta) T - ucos \alpha, v _{\perp}= eusin \alpha$
The time of flight while going down the inclined plane is
$T ^{\prime}=\frac{2 eusin \alpha}{ g \cos \beta}= eT$
The range of the projectile while going down is
$R =[(g \sin \beta) T - u \cos \alpha] e T +\frac{1}{2}(g \sin \beta) e ^{2} T ^{2}$
$\Rightarrow[(g \sin \beta) T -u \cos \alpha] e T+\frac{1}{2}(g \sin \beta) e ^{2} T ^{2}=(u \cos \alpha) T -\frac{1}{2}(g \sin \beta) T ^{2} $
$\Rightarrow u \cos \alpha(1+ e )=(g \sin \beta) T \left[\frac{1}{2}+ e +\frac{ e ^{2}}{2}\right]$
Substituting the value as $T=\frac{2 \text { usin } \alpha}{g \cos \beta}$ we get
$\Rightarrow \cot \alpha(1+ e )=2 \tan \beta\left[\frac{1}{2}+ e +\frac{ e ^{2}}{2}\right] $
$\Rightarrow 3 e ^{2}+2 e -1=0 $
$\Rightarrow e =\frac{1}{3} $ or $ \frac{1}{ e }=3$