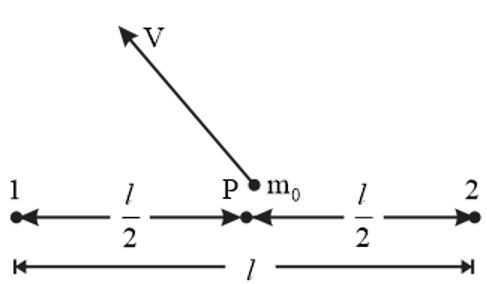
Q. A particle is projected from the mid-point of the line joining two fixed particles each of mass m. If the separation between the fixed particles is $l$ , the minimum velocity of projection of the particle so as to escape is equal to
NTA AbhyasNTA Abhyas 2020Gravitation
Solution: