Question

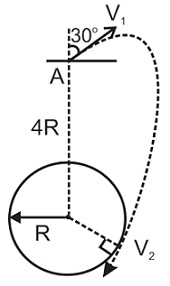
A particle is projected from point $A$ , that is at a distance $4R$ from the centre of the earth, with speed $v_{1}$ in a direction making $30^\circ $ with the line joining the centre of the earth and point $A$ , as shown. Find the speed $v_{1}$ if particle grazes the surface of the earth as shown in the figure. Consider gravitational interaction only between these two. (use $\frac{G M}{R}=6.4\times 10^{7} \, m^{2} \, s^{- 2}$ )

• A. $4\sqrt{2}kms^{- 1}$
• B. $3\sqrt{2}kms^{- 1}$
• C. $6\sqrt{2}kms^{- 1}$
• D. $5\sqrt{2}kms^{- 1}$

Answer 1

Answer: (A)

Conserving angular momentum w.r.t centre of earth,
$\left(\right.V_{1}cos 60 ^\circ \left.\right) \, 4 R = \left(mV\right)_{2} R$
$\Rightarrow \frac{V_{2}}{V_{1}}=2$
Conserving mechanical energy of the system,
$-\frac{G M m}{4 R}+\frac{1}{2}m V_{1}^{2}=-\frac{G M m}{R}+\frac{1}{2}m V_{2}^{2}$
$\frac{1}{2}V_{2}^{2}-\frac{1}{2} \, V_{1}^{2}=\frac{3}{4}\frac{G M}{R}$
$V_{1}^{2}=\frac{1}{2}\frac{G M}{R}$
$V_{1}=\frac{1}{\sqrt{2}} \, \sqrt{64 \times 10^{6}}=\frac{8000}{\sqrt{2}}ms^{- 1}=4\sqrt{2}kms^{- 1}$