Q.
A particle is oscillating on the X-axis with an amplitude $2 \,cm$ about the point $x_0=10 \, cm$, with a frequency $\omega$. A concave mirror of focal length 5 cm is placed at the origin (see figure).
Identify the correct statements.
(A) The image executes periodic motion.
(B) The image executes non-periodic motion.
(C) The turning points of the image are asymmetric w.r.t. the image of the point at $x = 10 \, cm$.
(D) The distance between the turning points of the oscillation of the image is $\frac{100}{21} $ cm.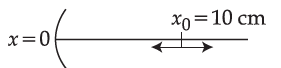
Solution:
