Q.
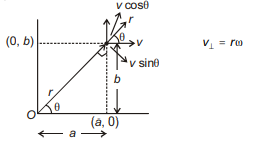
A particle is moving with constant speed $v$ in $x y$ plane as shown in figure. The magnitude of its angular velocity about point $O$ is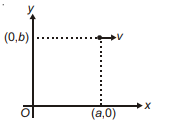
Motion in a Plane
Solution:
$v \sin \theta=r \omega$
$v \sin \theta=\sqrt{a^{2}+b^{2}} \times \omega$
$\frac{v}{\sqrt{a^{2}+b^{2}}} \frac{b}{\sqrt{a^{2}+b^{2}}}=\omega$
$\frac{v b}{\left(a^{2}+b^{2}\right)}=\omega$