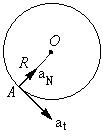
Question

A particle is moving in a circle of radius $R$ in such a way that at any instant the tangential retardation of the particle and the normal acceleration of the particle are equal. If its speed at $t=0 \,$ is $\, v_{0}$ , the time taken to complete the first revolution is

• A. $\frac{R}{v_{0}}$
• B. $\frac{R}{v_{0}}\left(\right.1-e^{- 2 \pi }\left.\right)$
• C. $\frac{R}{v_{0}}e^{- 2 \pi }$
• D. $\frac{2 \pi R}{v_{0}}$

Answer 1

Answer: (B)

When a particle moves in a circular motion, it is acted upon by centripetal force directed towards the centre. Hence, centripetal acceleration is
$a_{N}=\frac{d v}{d t}=\frac{v^{2}}{R}$
$or \, \, \int\limits _{0}^{t} \frac{d t}{R} = \int\limits _{v_{0}}^{v} \frac{d v}{v^{2}}$
$or \, \, \, t=-R\left[\frac{1}{v}\right]_{v_{0}}^{v}$
$v=\frac{v_{0} R}{R - v_{0} t}$
$Also \, \frac{d r}{d t}=\frac{v_{0} R}{\left(R - v_{0} t\right)}$
$\int\limits _{0}^{2 \pi \, R}dr=v_{0}R \, \int\limits _{0}^{T}\frac{d t}{R - v_{0} t}$
$\Longrightarrow \, \, \, T=\frac{R}{v_{0}}\left(1 - e^{- 2 \pi }\right) \, $