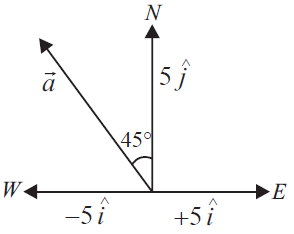
Q. A particle is moving eastward with velocity $5 \, m \, s^{-1}$ In 10 s the velocity changes to $5\, m\, s^{-1}$ northwards. The average acceleration in this time is
Solution:
Here, $ \vec{v_1} = 5\hat{i} \, m \, s^{-1} , \vec{v_2} = 5 \hat{j} \, m\, s^{-1}, t = 10 \, s$
$\vec{a} = \frac{\vec{v_2} - \vec{v_1}}{1} = \frac{5 \hat{j} - 5 \hat{i}}{10} = \frac{1}{2} ( j - i)$
$| \vec{a} | = \frac{1}{2} \sqrt{( -1)^2 + (1)^2}$
$ = \frac{1}{2} \sqrt{2} = \frac{1}{\sqrt{2}} m \, s^{-2}$
$\tan \theta=\frac{a_{y}}{a_{x}} = \left(\frac{\frac{1}{2}}{-\frac{1}{2}}\right)=-1 $
$ \theta=\tan^{-1} \left(-1\right) =135^\circ$
$ \therefore \:\:\: \vec{a} = \frac{1}{\sqrt{2}} m \, s^{-1}$ towards North West