Q. A particle is executing two different simple harmonic motions, mutually perpendicular of different amplitudes and having phase difference of $\frac{\pi}{2}$. The path of the particle will be :
BHUBHU 2003
Solution:
Let two perpendicular simple harmonic motions are
$x=A \sin (\omega t) \,\,\,...(1)$
$y=B \sin (\omega t+\phi) \,\,\,...(2)$
From Eq. (1) $ \sin (\omega t)=\frac{x}{A}$
$\Rightarrow \cos \omega t=\sqrt{1-\frac{x^{2}}{A^{2}}}$
From Eq. (2)
$\frac{y}{B}=\sin (\omega t) \cos \phi+\cos (\omega t) \sin \phi$
$=\left(\frac{x}{A}\right) \cos \phi+\sqrt{1-\frac{x^{2}}{A^{2}}} \sin \phi $
$\Rightarrow \frac{y}{B}-\frac{x}{A} \cos \phi=\sqrt{1-\frac{x^{2}}{A^{2}}} \sin \phi$
On squaring, we get
$=\frac{y^{2}}{B^{2}}+\frac{x^{2}}{A^{2}} \cos ^{2} \phi-\frac{2 x y}{A B} \cos \phi=\left(1-\frac{x^{2}}{A^{2}}\right) \sin ^{2} \phi $
$\Rightarrow \frac{y^{2}}{B^{2}}+\frac{x^{2}}{A^{2}}\left(\cos ^{2} \phi+\sin ^{2} \phi\right)-\frac{2 x y}{A B} \cos \phi=\sin ^{2} \phi$
$\Rightarrow \frac{x^{2}}{A^{2}}+\frac{y^{2}}{B^{2}}-\frac{2 x y}{A B} \cos \phi=\sin ^{2} \phi \,\,\,...(3) $
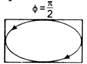
When, $\phi=\frac{\pi}{2}, \cos \phi=0, \sin \phi=1$
Hence, Eq. (3) reduces to
$\frac{x^{2}}{A^{2}}+\frac{y^{2}}{B^{2}}=1$
This presents the equation of symmetrical ellipse.