Q.
A particle having charge that of an electron and mass $1.6 \times 10^{-30} kg$ is projected with an initial speed $u$ at an angle $45^{\circ}$ to the horizontal from the lower plate of a parallel plate capacitor as shown in figure. The plates are sufficiently long and have separation $2\, cm$. The maximum value of velocity of particle not to hit the upper plate is $\sqrt{W} \times 10^{6} m / s$. Take electric field between the plates $=10^{3} V / m$ directed upward. The value of $W$ is _____.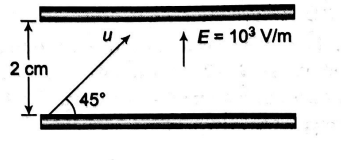
Electrostatic Potential and Capacitance
Solution:
