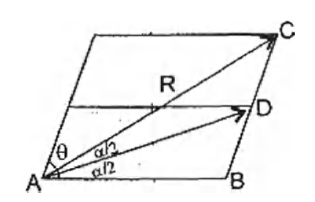
Q. A particle has two velocities of equal magnitude inclined to each other at an angle $theta$. If one of them is halved, the angle between the other and the original resultant velocity is bisected by the new resultant. Then $\theta$ is.
AIEEEAIEEE 2006Vector Algebra
Solution:
Let the magnitude of two velocities is $u$. We know that
$R=\sqrt{u^{2}+u^{2}+2u^{2}\,cos\,\theta}$
$R=\sqrt{2}u\sqrt{1+cos\,\theta}$
$R=2u\,cos \frac{\theta}{2}$
We know that by angle bisector theorem
$\frac{AB}{AC}=\frac{BD}{DC}$
$\Rightarrow \frac{u}{2u\,cos \frac{\theta}{2}}=1$
$cos \frac{\theta }{2}=\frac{1}{2}=cos \frac{\pi}{3}$
$\Rightarrow \theta=120^{°}$