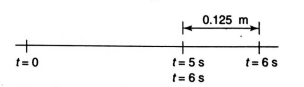
Question

A particle has an initial velocity of $5.5 \,ms^{-1}$ due east and a constant acceleration of $1 \,ms^{-2}$ due west. The distance covered by the particle in sixth second of its motion is

• A. 0
• B. 0.25 m
• C. 0.5 m
• D. 0.75 m

Answer 1

Answer: (B)

At $t = 5 \,s$
$S = 5.5 \times 5 \frac{1}{2} \times 1 \times (5)^2 $
$= 15\,m$
at $t = 6\,s$
$ S = 5.5 \times 6 - \frac{1}{2} \times 1 \times (6)^2 $
$= 15 \,m$
at $ t = 5.5\,s$
$S = 5.5 \times 5.5 - \frac{1}{2} \times 1 \times (5.5)^2 $
$= 15.125\,m$

Distance covered in $6$ th second
$= -2 \times 0.125 = 0.25 \,m$