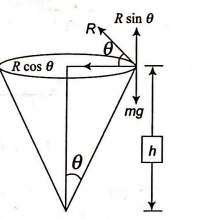
Question

A particle describes a horizontal circle in a conical funnel whose inner surface is smooth with speed of $0.5 \,m/s$. What is the height of the plane of circle from vertex of the funnel?

• A. $0.25 \,cm$
• B. $2 \,cm$
• C. $4 \,cm$
• D. $2.5 \,cm$

Answer 1

Answer: (D)

The particle is moving in circular path
From the figure, $mg =R \,sin\,\theta \ldots(i)$
$\frac{mv^{2}}{r}=R\,cos\, \theta \ldots(ii)$
From equation (i) and (ii) we get

$tan \,\theta = \frac{rg}{v^{2}}$ but $tan \,\theta = \frac{r}{h}$
$\therefore h=\frac{v^{2}}{g}=\frac{(0.5)^{2}}{10}$
$=0.025\,m=2.5\,cm$