Q.
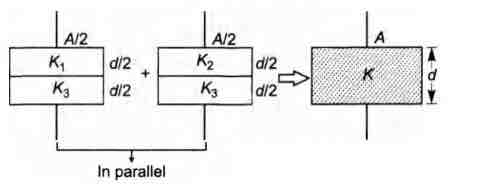
A parallel plate capacitor of area $A$, plate separation d and capacitance $C$ is filled with three different dielectric materials having dielectric constants $K_1,K_2 \, and \, K_3 $ as shown. If a single dielectric material is to be used to have the same capacitance $C$ in this capacitor then its dielectric constant $K$ is given by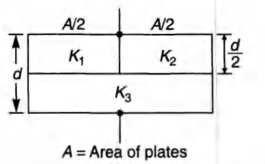
IIT JEEIIT JEE 2000Electrostatic Potential and Capacitance
Solution:
Applying C $= \frac {\varepsilon_0A}{d-t_1-t_2+ \frac {t_1}{K_1}+ \frac {t_2}{K_2}}, $ we have
$\frac {\varepsilon_0(A/2)}{d-d/2-d/2+ \frac {d/2}{K_1}+ \frac {d/2}{K_3}} $
$\, \, \, \, \, \, \, \, \, \, \, \, \, +\frac {\varepsilon_0(A/2)}{d-d/2-d/2+ \frac {d/2}{K_2}+ \frac {d/2}{K_3}}=\frac {K\varepsilon_0A}{d} $
Solving this equation, we get
$\, \, \, \, \, \, \, \, \, \, \, K= \frac {K_1K_3}{K_1+K_3}+ \frac {K_2K_3}{K_2+K_3} $