Q.
A parallel-plate capacitor made of circular plates, each of radius $R=6.0\, cm$, has a capacitance $C=100\, pF$. The capacitor is connected to $230 \, V$ a.c. supply with $a$ (angular) frequency of $300 \, rad / s$. Determine the amplitude of $B$ (in $10^{-11}\, T$ ) at a point $3.0\, cm$ from the axis between the plates.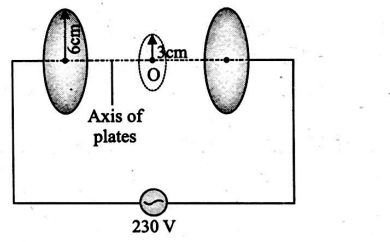
Electromagnetic Waves
Solution: