Q.
A parallel plate capacitor is made of two plates of length $I$, width $w$ and separated by distance $d$. A dielectric slab (dielectric constant K) that fits exactly between the plates is held near the edge of the plates. It is pulled into the capacitor by a force $F = - \frac{\partial U}{\partial\,x}$ where $U$ is the energy of the capacitor when dielectric is inside the capacitor up to distance $x$ (See figure). If the charge on the capacitor is $Q$ then the force on the dielectric when it is near the edge is :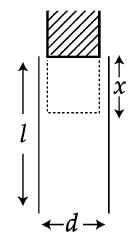
Solution: