Question

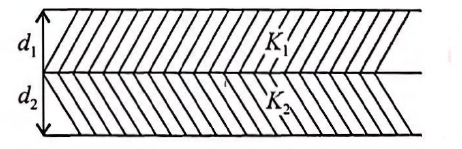
A parallel plate capacitor is made of two dielectric blocks in series. One of the blocks has thickness $d_{1}$ and dielectric constant $K_{1}$ and the other has thickness $d_{2}$ and dielectric constant $K_{2}$ as shown in figure. This arrangement can be thought as a dielectric slab of thickness $d (= d_{1} + d_{2})$ and effective dielectric constant $K$. The $K$ is

• A. $\frac{K_{1} d_{1}+K_{2}d_{2}}{d_{1}+d_{2}}$
• B. $\frac{K_{1} d_{1}+K_{2}d_{2}}{K_{1}+K_{2}}$
• C. $\frac{K_{1}K_{2}\left(d_{1}+d_{2}\right)}{K_{2}d_{1}+K_{1}d_{2}}$
• D. $\frac{2 K_{1}K_{2}}{K_{1}+K_{2}}$

Answer 1

Answer: (C)

The capacities of two individual condensers are
$C_{1}=\frac{K_{1}\varepsilon_{0} A}{d_{1}}$ and $C_{2}=\frac{K_{2}\varepsilon_{0}A}{d_{2}}$
The arrangement is equivalent to two capacitors joined in series
$\therefore $ Equivalent capacitance, $\frac{1}{C_{eq}}=\frac{1}{C_{1}}+\frac{1}{C_{2}}$,
$=\frac{d_{1}}{K_{1}\varepsilon_{0} A}+\frac{d_{2}}{K_{2} \varepsilon_{0} A}$
$=\frac{1}{\varepsilon_{0} A} \left[\frac{d_{1}}{K_{1}}+\frac{d_{2}}{K_{2}}\right]=\frac{1}{\varepsilon_{0} A} \left[\frac{K_{2}d_{1}+K_{1}d_{2}}{K_{1}K_{2}}\right]$
or $C_{eq}=\varepsilon_{0}A \left(\frac{K_{1}K_{2}}{K_{2}d_{1}+K_{1}d_{2}}\right)\ldots\left(i\right)$
Also $C_{eq}=\frac{K \varepsilon_{0}A}{d_{1}+d_{2}} \ldots\left(ii\right)$
From $\left(i\right)$ and $\left(ii\right)$
$\varepsilon_{0}A \left(\frac{K_{1} K_{2}}{d_{2}K_{1}+d_{1} K_{2}}\right)=\varepsilon_{0}A \left(\frac{K}{d_{1} +d_{2}}\right)$
$\therefore K=\frac{K_{1}K_{2}\left(d_{1}+d_{2}\right)}{d_{2}K_{1}+d_{1}K_{2}}$