Question

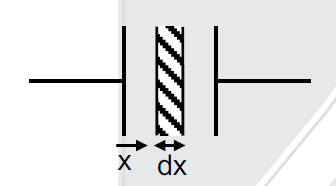
A parallel plate capacitor has plates of area A separated by distance $'d'$ between them. It is filled with a dielectric which has a dielectric constant that varies as $k\left(x\right) = K\left(1+\alpha x\right)$ where 'x ' is the distance measured from one of the plates. If $\left(\alpha d \right) < < 1,$, the total capacitance of the system is best given by the expression :

• A. $\frac{A\epsilon_{0}K}{d}\left(1+\left(\frac{\alpha d}{2}\right)^{2}\right)$
• B. $\frac{AK\epsilon_{0}}{d}\left(1+\frac{\alpha d}{2}\right)$
• C. $\frac{A\epsilon_{0}K}{d}\left(1+\frac{\alpha^{2}d^{2}}{2}\right)$
• D. $\frac{AK\epsilon_{0}}{d}\left(1+\alpha d\right)$

Answer 1

Answer: (B)

Capacitance of element $=\frac{k\varepsilon_{0}A}{dx}$
Capacitance of element, $C' =\frac{k_{0}\left(1+\alpha x\right)\varepsilon_{0}\,A}{dx}$
$\sum \frac{1}{C'}=$$\int\limits^{d}_{{0}}$$\frac{dx}{k_{0}\varepsilon_{0}A\left(1+\alpha x\right)}$
$\frac{1}{C}=\frac{1}{k_{0}\varepsilon_{0}A\alpha}\ell n\left(1+\alpha d\right)$
Given $\alpha d < < 1$
$\frac{1}{C}=\frac{1}{k_{0}\varepsilon_{0}A\alpha}\left(\alpha d-\frac{\alpha^{2}d^{2}}{2}\right)$
$\frac{1}{C}=\frac{d}{k_{0}\varepsilon_{0}A }\left(1-\frac{\alpha d}{2}\right)$
$C=\frac{k_{0}\varepsilon_{0}A}{d}\left(1+\frac{\alpha d}{2}\right)$