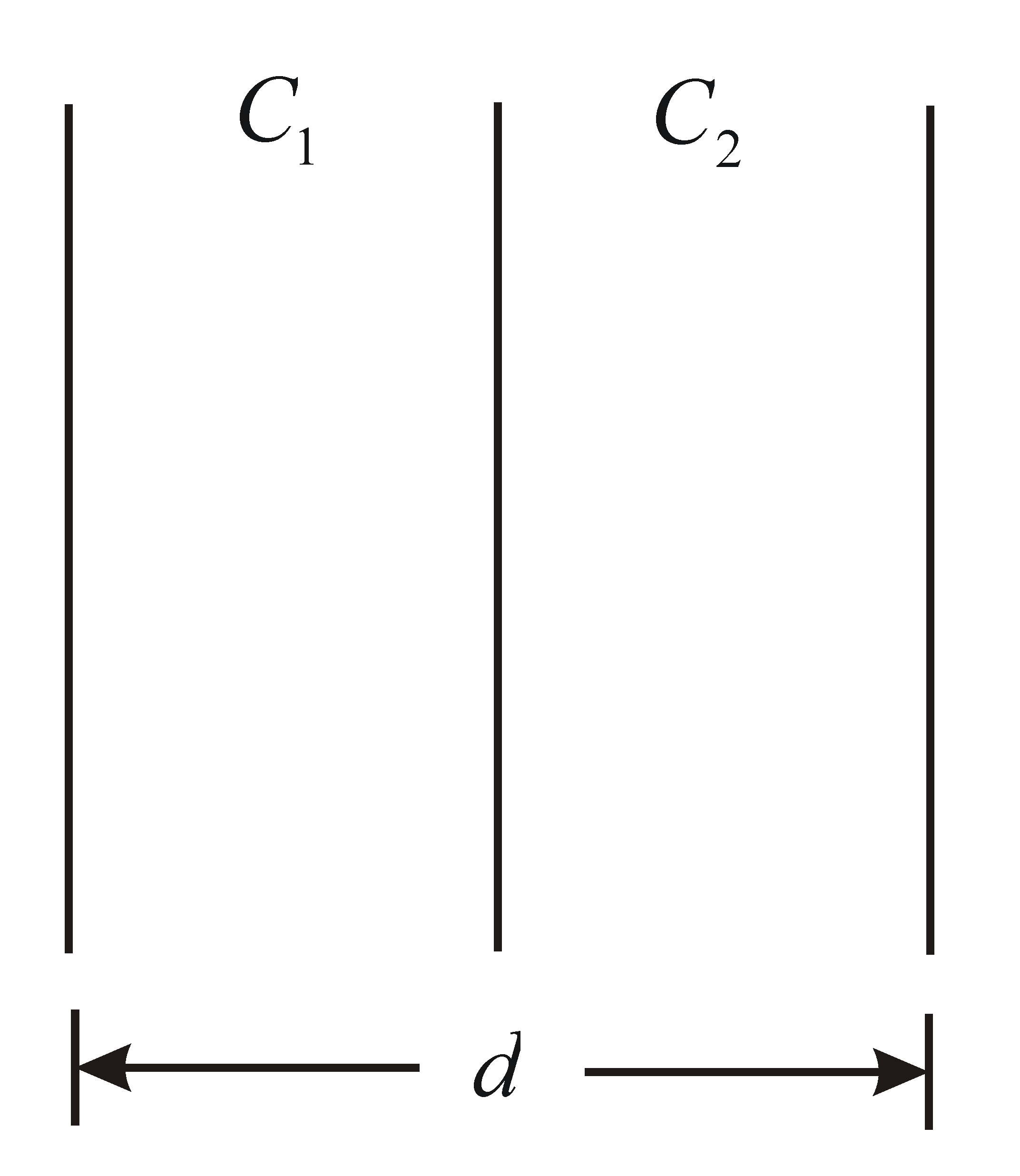
Question

A parallel plate air capacitor has a capacitance $C$ . When it is half-filled with a dielectric constant $5$ , the percentage increase in the capacitance will be

• A. $400\%$
• B. $66.6 \, \%$
• C. $33.3 \, \%$
• D. $200 \, \%$

Answer 1

Answer: (B)

Initial capacitance
$ C=\frac{\epsilon _{0} A}{d}$

When it is half filled by a dielectric of dielectric constant $K$, then
$C _1=\frac{K \epsilon_0 A}{d / 2}=2 K \frac{\epsilon_0 A}{d}$
and $C_2=\frac{\epsilon_0 A}{d / 2}=\frac{2 \epsilon_0 A}{d}$
$\therefore \frac{1}{C^{\prime \prime}}=\frac{1}{C_1}+\frac{1}{C_2} $
$=\frac{d}{2(\epsilon)_0 A}\left(\frac{1}{K}+1\right)=\frac{d}{2(\epsilon)_0 A}\left(\frac{1}{5}+1\right) $
$=\frac{6}{10} \frac{d}{\epsilon_0 A}$
$\therefore C^{\prime \prime}=\frac{5 \epsilon_0 A}{3 d}$
Hence, increase in capacitance
$=\frac{\frac{5}{3} \frac{\epsilon_0 A}{d}-\frac{\epsilon_0 A}{d}}{\frac{\epsilon_0 A}{d}}=\frac{5}{3}-1=\frac{2}{3}=66.6 \%$