Question

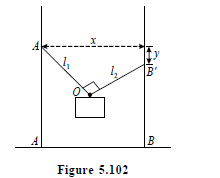
$A O B$ is a swing suspended from vertical poles $A A^{\prime}$ and $B B^{\prime}$ as shown. If ropes $O A^{\prime}$ and $O B$ of length $l_{1}$ and $l_{2}$ respectively are massless, and are perpendicular to each other with a point mass $m$ hanging from $O$, the time period of the swing for small oscillations perpendicular to the plane of paper is:

• A. $2 \pi \sqrt{\frac{l_{1} l_{2}}{g \sqrt{x^{2}+y^{2}}}}$
• B. $2 \pi \sqrt{\frac{\left(x^{2}+y^{2}\right)^{3 / 2}}{l_{1} l_{2} g}}$
• C. $2 \pi \sqrt{\frac{x^{2}+y^{2}}{\sqrt{l_{1} l_{2}} g}}$
• D. $2 \pi \sqrt{\frac{l_{1} l_{2}}{x \cdot g}}$

Answer 1

Answer: (D)

The system acts as a pendulum of length $l$ acting under effective gravity of $g \cos \theta$ as shown in figure
Now, $l_{1} l_{2}=A B . l=\sqrt{x^{2}+y^{2}} \cdot l$
$\cos \theta=\frac{x}{\sqrt{x^{2}+y^{2}}}$

$\Rightarrow T=\sqrt{\frac{l_{1} l_{2} \sqrt{x^{2}+y^{2}}}{\sqrt{x^{2}+y^{2}} \cdot g x}}=2 \pi \sqrt{\frac{l_{1} l_{2}}{g x}}$