Question

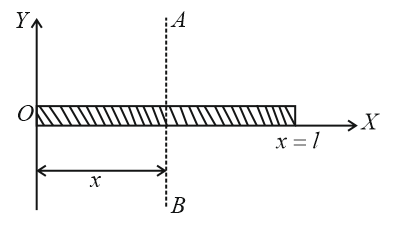
A nonuniform rod $OM$ (of length $L$ ) is kept along $x$ -axis and is rotating about an axis $AB$ , which is perpendicular to rod as shown in the figure. The rod has linear mass density that varies with the distance $x$ from left end of the rod according to $\lambda =\left(\lambda \right)_{0}\left(\frac{x^{3}}{L^{3}}\right);$ where $\lambda _{0}$ is constant. If the value of $x=\frac{K L}{5}$ so that moment of inertia of rod about axis $AB$ $\left(I_{A B}\right)$ is minimum. Find the value of $K$ .

Answer 1

We know from our concept of moment of inertia, that moment of inertia will be minimum, when it rotates about an axis passes through centre of mass of body, so in this question, axis $AB$ must pass through centre of mass, so we have to find centre of mass of body,
Centre of mass of body for non-uniform distributed mass is given by,
$x_{C M}=\frac{\int x d m}{\int d m}$
$\Rightarrow x_{C M}=\frac{\int x(\lambda d x)}{\int(\lambda d x)}$
$\Rightarrow x_{C M}=\frac{\int x\left(\lambda_{0}\left(\frac{x^{3}}{L^{3}}\right)\right) d x}{\int\left(\lambda_{0}\left(\frac{x^{3}}{L^{3}}\right) d x\right)}$
$\Rightarrow x_{C M}=\frac{\int x\left(\frac{x^{3}}{L^{3}}\right) d x}{\int\left(\frac{x^{3}}{L^{3}}\right) d x}$
$\Rightarrow x_{C M}=\frac{\int\limits_{0}^{L} x^{4} d x}{\int\limits_{0}^{L} x^{3} d x}$
$\Rightarrow x_{C M}=\frac{\left[\frac{x^{5}}{5}\right]_{0}^{L}}{\left[\frac{x^{4}}{4}\right]_{0}^{L}}$
$\Rightarrow x_{C M}=\frac{\frac{L^{5}}{5}}{\frac{L^{4}}{4}}$
$\Rightarrow x_{C M}=\frac{4 L}{5}$
On comparing from above given relation, $K=4$ .