Q.
A non-zero current passes through the galvanometer $G$ shown in the circuit when the key ‘$K$’ is closed and its value does not change when the key is opened. Then which of the following statement(s) is/are true ?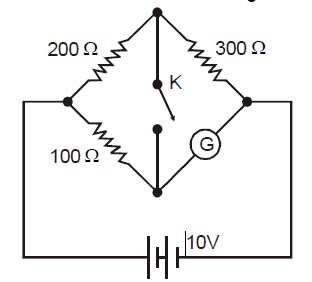
Solution:

Solution:
