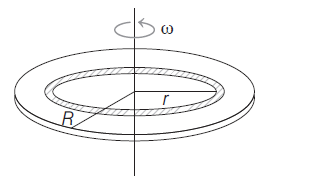
Question

A non-conducting thin disc of radius $R$ rotates about its axis with an angular velocity $\omega$. The surface charge density on the disc varies with the distance $r$ from the centre as $\sigma(r)=\sigma_{0}\left[1+\left(\frac{r}{R}\right)^{\beta}\right]$, where $\sigma_{0}$ and $\beta$ are
constants. If the magnetic induction at the center is $B=\left(\frac{9}{10}\right) \,\mu_{0} \,\sigma_{0} \,\omega R$, the value of $\beta$ is

• A. $\frac{1}{4}$
• B. $4$
• C. $\frac{1}{2}$
• D. $2$

Answer 1

Answer: (A)

Total charge on the disc, $Q=\sigma\left(\pi R^{2}\right)$
Period of motion, $T=2 \pi / \omega$

So, current in the ring, $d I=\frac{d Q}{T}$
$\because Q=\sigma \pi R^{2} \Rightarrow d Q=2 \,\sigma \,\pi \,r d r $
$\therefore d I=\frac{2 \sigma \pi r d r}{2 \pi} \times \omega=\sigma \,\omega \,r d r $
Magnetic field due to ring is
$d B=\frac{\mu_{0} \,d \,I}{2 r}$
So, magnetic field due to disk is
$B=\int d B=\int_{0}^{R} \frac{\mu_{0}}{2 r} \cdot \sigma \,\omega \,r d r$
On putting value of $\sigma$, we get
$B =\frac{\mu_{0} \,\sigma_{0} \,\omega}{2} \int_{0}^{R}\left[^{1}+\left(\frac{r}{R}\right)^{\beta}\right] d r $
$=\frac{\mu_{0}\, \sigma_{0}\, \omega}{2}\left[R+\frac{R^{\beta+1}}{R^{\beta}(1+\beta)}\right]=\frac{\mu_{0} \,\sigma_{0} \,\omega}{2} \times\left(\frac{2+\beta}{1+\beta}\right) R$
Now,
$ B=\frac{9}{10} \,\mu_{0}\, \sigma_{0}\, \omega R=\frac{\mu_{0}\,\sigma_{0} \,\omega R}{2} \times \frac{(2+\beta)}{(1+\beta)}$
$\Rightarrow 5 \beta+10=9 \beta+9$
$\Rightarrow \beta=\frac{1}{4}$