Question

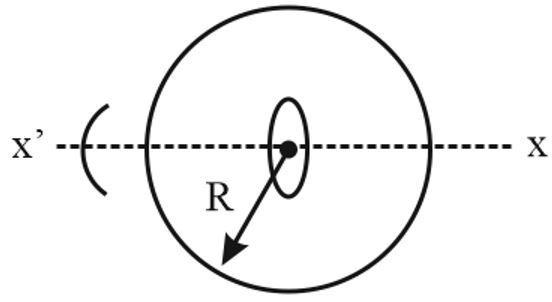
A non-conducting ring of radius $R$ having uniformly distributed charge $Q$ starts rotating about $x-x'$ axis passing through diameter with an angular acceleration $\alpha $ , as shown in the figure. Another small conducting ring having radius $a$ $\left(a \ll R\right)$ is kept fixed at the centre of the bigger ring is such a way that axis $xx'$ is passing through its centre and perpendicular to its plane. If the resistance of the small ring is $r=1 \, \Omega ,$ find the induced current in it in $ampere$ .

(Given $q=\frac{16 \times 1 0^{2}}{\mu _{0}} \, C,$ $R=1 \, m, \, a \, = \, 0.1 \, m$ , $\alpha =8 \, rad \, s^{- 2}$ )

Answer 1

$d q=\frac{q}{2 \pi R} \cdot R d \theta=\frac{q}{2 \pi} \cdot d \theta$
$d i=\frac{d q}{T}=\frac{q d \theta \omega}{2 \pi 2 \pi}$
$d i=\frac{q \omega}{4 \pi^{2}} \cdot d \theta$
$d B=\frac{\mu_{0} d i(R \sin \theta)^{2}}{2 R^{3}}$
$\int d B=\int_{0}^{\pi} \frac{\mu_{0} \sin ^{2} \theta}{2 R}\left(\frac{q \omega}{4 \pi^{2}}\right) d \theta$
$B=\frac{\mu_{0} q \omega}{16 \pi R}$
$\phi=B \pi a^{2}$
$\phi=\pi a^{2} \cdot \frac{\mu_{0} q \omega}{16 \pi R}$
$\phi=\frac{\mu_{0} q \omega a^{2}}{16 R}$
$|\varepsilon|=\left|\frac{d \phi}{d t}\right|_{2}$
$\varepsilon \mid=\frac{\mu_{0} q a^{2}}{16 R} \alpha$
$=8$ volt
$i=\frac{8}{1}=8 A$