Q.
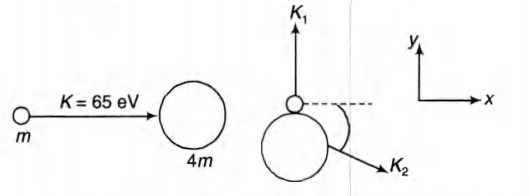
A neutron of kinetic energy 65 eV collides melastically with
a singly ionized helium atom at rest. It is scattered at an angle
o f $90^\circ$ with respect of its original direction
(a) Find the allowed values of the energy of the neutron and
that of the atom after the collision
(b) If the atom gets de-excited subsequently by emitting
radiation, find the frequencies of the emitted radiation.
[Given : Mass of He atom : $4 \times$ (mass of neutrons )
Ionization energy of H atom = 13.6 eV]
IIT JEEIIT JEE 1993
Solution:
(a) Let $k_1$,and $K_2$ be the kinetic energies of neutron and
helium atom after collision and $\Delta E$ be the excitation
energy.
From conservation of linear momentum along
x-direction.
$\, \, \, \, \, \, \, p_i = pf$
$\rightarrow \sqrt{2Km} = \sqrt {2(4m)K_2} cos
heta \, \, \, \, \, \, ...(i)$
Similarly, applying conservation of linear momentum in
$y$ - direction, we have
$\sqrt{2K_1m}= = \sqrt {2(4m)K_2}cos
heta \, \, \, \, ...(ii)$
Squaring and adding Eqs. (i) and (ii), we get
$ \, \, \, K + k_1 = 4K_2 \, \, \, ...(iii)$
or $ \, \, \, \, 4K_2 - K_1 = K = 65eV \, \, \, \, ...(iv)$
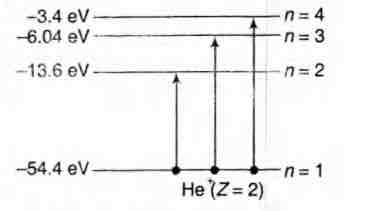
Now, during collision, electron can be excited to any
higher energy state. Applying conservation of energy,
we get $K = K_1 + K_2 + \Delta E$
or $65 = k_1 + K_2 + \Delta E \, \, \, \, ...(v)$
$\Delta E$ can have the following values
$\Delta E_1 = {- 1.6 - (- 54.4)} eV = 40.8 eV$
Substituting in (v), we get
$K _1 + K_2 = 24.2 eV \, \, \, \, \, ...(vi)$
Solving (iv) and (vi), we get
$ \, \, \, \, \, \, \, \, \, \, K_1 = 6.36 eV$
and $K_2 = 17.84 eV$
Similarly, when we put $\Delta E = $\Delta E_2$
$= {- 6.04 - (- 6.04 - (-54.4)}eV
$= 48.36eV$
Put in Eq. (v), wc get
$ K_1 + K_2 = 16.64 $ e V $$ ...(vii)
Solving Eqs. (iv) and (vii), we get
$K_1$ = 0.312 eV and $K_2$ = 16.328 eV
Similarly, when we put
$\triangle E = \triangle E_3$ = {-3.4 - (-54.4)} = 51 eV
Put in Eq. (v), we get
$ K_1 + K_2 = 14$ e V $$ ...(viii)
Now, solving Eqs. (iv) and (viii), we get
$K_1$ ,= -1.8 eV and $K_2$ = 15.8 eV
But since the kinetic energy cannot have the negative values,
the electron will not jump to third excited state or n = 4.
Therefore, the allowed values of $K_1$ ,(KE of neutron) are
6.36 eV and 0.312 eV and of $K_2$ (KE of th. atom) are 17.84
eV and 16.328 eV and the electron can jump upto second
excited state only (n = 3).
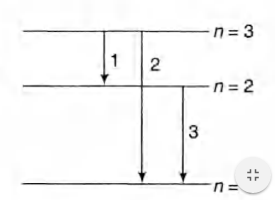
(b) Possible emission lines are only three as hown in
figure. The corresponding
frequencies are
$ v_1 = \frac{( E_3 - E_2 )}{ h} $
= $ \frac{ \{ - 6.04 - (- 13 . 6) \} \times 1.6 \times 10^{ - 19}}{ 6.63 \times 10^{ - 34}} $
= $ 1.82 \times 10^{15} $ Hz
$ v_2 = \frac{ E_3 - E_1}{ h} = \frac{ \{ - 6.04 - (- 54.4) \} \times 1.6 \times 10^{ - 19}}{ 6.63 \times 10^{ - 34}} $
= $ 11.67 \times 10^{15}$ Hz
and $ v_3 = \frac{ E_2 - E_1}{ h} $
= $ \frac{ \{ - 13.6 - (- 54.4 ) \} \times 1.6 \times 10^{ - 19}}{ 6.63 \times 10^{ - 34}} $
= $ 9.84 \times 10^{ 15}$ Hz
Hence, the frequencies of emitted radiations are
$ 1.82 \times 10^{15} Hz, \, 11.67 \times 10^{ 15} Hz \, and \, 9.84 \times 10^{ 15} $ Hz.