Q.
A network of four capacitors of capacity equal to $C_{1}=C, C_{2}=2 C, C_{3}=3 C$ and $C_{4}=4 C$ are connected to a battery as shown in the figure. The ratio of the charges on $C_{2}$ and $C_{4}$ is.: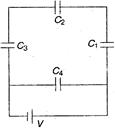
Delhi UMET/DPMTDelhi UMET/DPMT 2006
Solution: