Q.
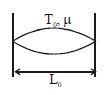
A musical instrument is made using four different metal strings, 1, 2, 3 and 4 with mass per unit length $\mu$, 2$\mu$, 3$\mu$ and 4$\mu$ respectively. The instrument is played by vibrating the strings by varying the free length in between the range $L_0$ and $2L_0$. It is found that in string-1 ($\mu$) at free length $L_0$ and tension $T_0$ the fundamental mode frequency is $f_0$.
List-I gives the above four strings while list-II lists the magnitude of some quantity.
List-I
List-II
(I) String-1 ($\mu$)
(p) 1
(II) String-2 (2$\mu$)
(Q) 1/2
(III) String-3 (3$\mu$)
(R) $1/\sqrt{2}$
(IV) String-4 (4$\mu$)
(S) $1/\sqrt{2}$
(T)3/16
(U) 1/16
Question: The length of the strings 1, 2, 3 and 4 are kept fixed at $L_0$, $\frac{3L_{0}}{2}, \frac{5L_{0}}{4},$ and $\frac{7L_{0}}{4},$ respectively. Strings 1, 2, 3, and 4 are vibrated at their $1^{st}$, $3^{rd}$, $5^{th}$ and $14^{th}$ harmonics, respectively such that all the strings have same frequency. The correct match for the tension in the four strings in the units of $T_0$ will be,
| List-I | List-II |
|---|---|
| (I) String-1 ($\mu$) | (p) 1 |
| (II) String-2 (2$\mu$) | (Q) 1/2 |
| (III) String-3 (3$\mu$) | (R) $1/\sqrt{2}$ |
| (IV) String-4 (4$\mu$) | (S) $1/\sqrt{2}$ |
| (T)3/16 | |
| (U) 1/16 |
JEE AdvancedJEE Advanced 2019
Solution:
For string (1)
Length of string = $L_0$
It is vibrating in $I^{st}$ harmonic i.e. fundamental mode.
$f_{0} = \frac{1}{2L_{0}}\sqrt{\frac{T_{0}}{\mu}}\Rightarrow \left(P\right)$
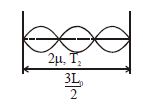
For string (2)
Length of string $= \frac{3L_{0}}{2}$
It is vibrating in $III^{rd}$ harmonic but frequency is still $f_{0}$.
$f_{0} = \frac{3v}{2L}$
$f_{0} = \frac{3}{2\left(\frac{3L_{0}}{2}\right)}\sqrt{\frac{T_{2}}{2\mu}}$
$\Rightarrow \,f_{0} = \frac{1}{L_{0}}\sqrt{\frac{T_{2}}{2\mu}} = \frac{1}{2L_{0}}\sqrt{\frac{T_{0}}{\mu}}$
$\Rightarrow \,T_{2} = \frac{T_{0}}{2}\,\Rightarrow \quad\left(Q\right)$
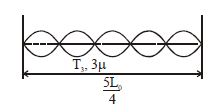
For string (3)
Length of string $= \frac{5L_{0}}{4}$
It is vibrating in $5^{th}$ harmonic but frequency is still $f_{0}.$
$f_{0} = \frac{5V}{2L}$
$\Rightarrow \, f_{0} = \frac{5}{2\left(\frac{5L_{0}}{4}\right)}\sqrt{\frac{T_{3}}{3\mu}} = \frac{1}{2L_{0}}\sqrt{\frac{T_{0}}{\mu}}$
$\Rightarrow \, \frac{2}{L_{0}}\sqrt{\frac{T_{3}}{3\mu}} = \frac{1}{2L_{0}}\sqrt{\frac{T_{0}}{\mu}}$
$T_{3} = \frac{3T_{0}}{16} \Rightarrow \left(T\right)$
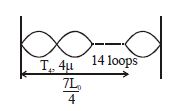
For string (4)
Length of string $= \frac{7L_{0}}{4}$
It is vibrating in $14^{th}$ harmonic but frequency is still $f_{0}$.
$f_{0} = \frac{14}{2L}$
$\Rightarrow \quad f_{0} = \frac{14}{2\left(\frac{7L_{0}}{4}\right)}\sqrt{\frac{T_{4}}{4\mu}} = \frac{1}{2L_{0}}\sqrt{\frac{T_{0}}{\mu}}$
$\Rightarrow \frac{4}{L_{0}}\sqrt{\frac{T_{4}}{4\mu}} = \frac{1}{2L_{0}}\sqrt{\frac{T_{0}}{\mu}} \Rightarrow T_{4} = \frac{T_{0}}{16}\,\Rightarrow \left(U\right)$