Question

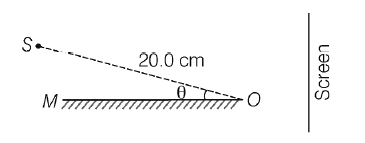
A monochromatic light source $S$ of wavelength $440\, nm$ is placed slightly above a plane mirror $M$ as shown below. Image of $S$ in $M$ can be used as a virtual source to produce interference fringes on the screen. The distance of source $S$ from $O$ is $20.0\, cm$ and the distance of screen from $O$ is $100.0\, cm$ (figure is not to scale). If the angle $0 = 0.50$ x $10^{-3}$ radians , then the width of the interference fringes observed on the screen is

• A. 2.20 mm
• B. 2.64 mm
• C. 1.10 mm
• D. 0.55 mm

Answer 1

Answer: (B)

Given arrangement is

Angle $\, \theta=0.5\times10^{-3}$radians.
SO, distance between source $S$ and its image $S_1$ is
$d=2r\theta=2\times SO\times\theta$
$=2\times20\times0.5\times10^{-3}$cm
$=20\times10^{-3}cm=2\times10^{-4} m$
Distance of sources $S$ and $S_1$ from screen
$D=a +b=20+100=120\, cm$
$=120\times10^{-2}m$
Wavelength of light used is
$\lambda=440\,nm=440\times10^{-9}m$
Both $S$ and $S_1$ acts like slits (sources of coherent light) and produces fringes over screen.
Width of a fringe, $\beta=\frac{\lambda D}{d}$
$\therefore \beta = \frac{440\times10^{-9}\times120\times10^{-2}}C$
$=2.64\, mm$