Q.
A metre stick swinging in vertical plane about a fixed horizontal axis passing through its one end undergoes small oscillation of frequency $f_{0}$. If the bottom half of the stick were cut off, then its new frequency of small oscillation would become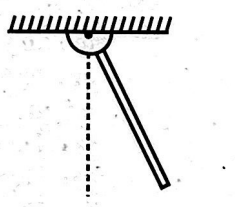
Oscillations
Solution: