Q.
A metal bar AB can slide on two parallel thick metallic rails separated by a distance I. A resistance R and an inductance L are connected to the rails as shown in the figure. A long
straight wire, carrying a constant
current 70 is placed in the plane of
the rails as shown. The bar AB is
held at rest at a distance xQ from the long wire. At t = 0, it made
to slide on the rails away from the wire. Answer the following
questions.
(a) Find a relation among i,$\frac{di}{dt}$ and $\frac{d\phi}{dt}$ where i is the current
in the circuit and $\phi$ is the flux of the magnetic field due to
the long wire through the circuit.
(b) It is observed that at time $t = T$, the metal bar AB is at a
distance of 2x$_0$ from the long wire and the resistance $R$
carries a current Obtain an expression for the net
charge that has flown through resistance $R$ from $t = 0$ to
t = T.
(c) The bar is suddenly stopped at time $T$. The current
through resistance R is found to be $t_1$,/4 at time 2T.
Find the value of L/R in terms of the other given quantities.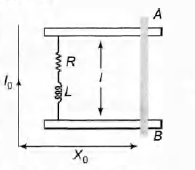
IIT JEEIIT JEE 2002
Solution: