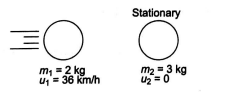
Question

A metal ball of mass $2 \, kg$ moving with speed of $36\, km / h$ has a collision with a stationary ball of mass $3\, kg$. If after collision, both the ball move together, the loss in kinetic energy due to collision is:

• A. $80\, J$
• B. $40\, J$
• C. $60 \, J$
• D. $160 \, J$

Answer 1

Answer: (C)

After collision the metal ball sticks with a stationary ball, then the kinetic energy is lost in other forms of heat, hence in this process of in elastic collision the kinetic energy is not conserved (only total energy is conserved) but momentum is conserved.
From law of conservation of momentum, we have
$ m_1 u_1+m_2 u_2=\left(m_1+m_2\right) v $
$\Rightarrow v=\frac{m_1 u_1+m_2 u_2}{\left(m_1+m_2\right)}$
Given, $ m=2 \,kg , u_1=36 \times \frac{5}{18}=10 \, m / s ,$
$ m_2=3 \, kg , u_2=0$

$\therefore \quad v=\frac{2 \times 10+3 \times 0}{2+3}=4 m / s$
Loss in kinetic energy is $\Delta K=\Delta K^{\prime}-\Delta K^{\prime \prime}$
$= \left\{\frac{1}{2} m_1 u_1^2+\frac{1}{2} m_2 u_2^2\right\}-\left\{\frac{1}{2}\left(m_1+m_2\right) v^2\right\} $
$= \left\{\frac{1}{2} \times 2 \times(10)^2+\frac{1}{2} \times 3 \times 0\right\}$
$ -\left\{(2+3) \times \frac{1}{2} \times(4)\right\} $
$ = 100-40=60 \,J $