Question

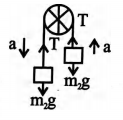
A massless string passing over a friction less pulley and carries two masses $m _{1} \& m _{2}$ $\left(m_{1}>m_{2}\right)$ at its ends. If $g$ is the acceleration due to gravity then the thrust on the pulley is $\left(m_{1}>m_{2}\right)$

• A. $\left(\frac{4 m_{1} m_{2}}{m_{1}+m_{2}}\right) g$
• B. Zero
• C. $\left(\frac{2 m_{1} m_{2}}{m_{1}+m_{2}}\right) g$
• D. $\left(\frac{2 m_{1} m_{2}}{m_{1} m_{2}}\right) g$

Answer 1

Answer: (A)

Equations of motion are
$m _{1} g - T = m _{1} a \ldots (i) $
$T - m _{2} g = m _{2} a \ldots (ii)$
From eq (i) $T =- m _{1} a + m _{1} g$
$-m_{1} a+m_{1} g-m_{2} g=m_{2} a$
$m_{1} g-m_{1} a=m_{2} a+m_{2} g$
$g\left(m_{1}-m_{2}\right)=a\left(m_{1}+m_{2}\right)$
Putting the value of $a$ in eq (i) we get
$m _{1} g - T =\frac{ m _{1}\left( m _{1}- m _{2}\right) g }{\left( m _{1}+ m _{2}\right)}$
$m _{1} g - T =\frac{\left( m _{1}^{2}- m _{1} m _{2}\right) g }{\left( m _{1}+ m _{2}\right)} $
$\Rightarrow \left( m _{1}+ m _{2}\right)\left( m _{1} g - T \right) $
$=\left( m _{1}^{2}- m _{1} m _{2}\right) g $
$\therefore m _{1}^{2} g - m _{1} T + m _{1} m _{2} g - m _{2} T = m _{1}^{2} g - m _{1} m _{2} g$
$ m _{1}^{2} g - m _{1} T + m _{2} m _{1} g - m _{2} T = m _{1}^{2} g + m _{1} m _{2} g =0$
$- T \left( m _{1}+ m _{2}\right)+2 m _{1} m _{2} g =0$
$\frac{2 m _{1} m _{2}}{ m _{1}+ m _{2}} g = T$
Thrust on the pulley is $2 T$
$\therefore $ Thrust is equal to
$\frac{4 m _{1} m _{2} g }{ m _{1}+ m _{2}}$